人工智能数学基础:求导神器--罗必塔法则


一、引言
如果两个函数f(x)、F(x)在x->a或x->∞时,其值都趋于0或无穷大,,那么这两个函数的商为0/0或∞/∞,那么f(x)/F(x)在x->a或x->∞时的极限可能存在、也可能不存在,通常把这种极限叫做未定式,并分别简记为:
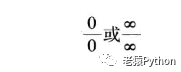
罗必塔(L’Hospital)法则,也称为洛必达法则,就是针对这种未定式极限中某些有极限值的部分未定式来推理其极限的简单重要方法。
二、罗必塔法则
2.1、定理1
1、定理
设:
当x->a时,函数f(x)和F(x)都趋于0;
在点a的某去心邻域内,f’(x)和F’(x)都存在,且F’(x)不等于0;
x->a时,lim(f’(x)/F’(x))存在(或为无穷大)。
则:
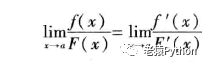
2、证明思路
由于是求lim(f(x)/F(x))的极限,当x->a时,函数f(x)和F(x)都趋于0,且当x->a时,函数f(x)和F(x)都趋于0,因此不妨假设f(a)=F(a)=0。因此两个函数在点a的邻域内是连续的,即:
函数f(x)和F(x)在[x,a]内连续,由条件2指定二者在(x,a)内可导,且F’(x)不等于0,因此满足柯西中值定理的要求,则函数f(x)和F(x)在(x,a)内,下列等式成立:
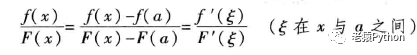
当x->a时,ε->a,对上式两端求极限,即可得到证明。
3、意义
洛必达法则,对于未定式求极限时,如果在x->a时,当lim(f’(x)/F’(x))存在或趋于无穷大时,lim(f(x)/F(x))也存在或趋于无穷大,且其极限等于lim(f’(x)/F’(x))。
如果当lim(f’(x)/F’(x))也是未定式,且(f’(x)和F’(x)满足定理的条件时,那么可以继续使用洛必达法则,通过lim(f"(x)/F"(x))求得lim(f’(x)/F’(x)),再求得lim(f(x)/F(x))。
通过以上方式,可以实现极限运算求解的降维操作,从而化繁为简实现快速求取极限。
2.2、定理2
定理1的x->a时改为x->∞,也有相应的罗必塔法则:
设:
当x->∞时,函数f(x)和F(x)都趋于0;
当|x|>N时,f’(x)和F’(x)都存在,且F’(x)不等于0;
x->∞时,lim(f’(x)/F’(x))存在(或为无穷大)。
则:
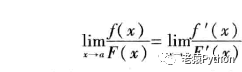
三、案例
洛必达法则是求未定式的一种有效方法,但最好能与其他求极限的方法结合使用。例如能化简时应尽可能先化简,可以应用等价无穷小替代或重要极限时,应尽可能应用,这样可以使运算简捷。

四、小结
本文介绍了罗必塔法则的内容,罗必塔法则给出的是求未定式的一方法,通过对满足条件的两个函数的商求导后的结果求极限,作为未定式的极限。
当定理条件满足时,所求的极限当然存在(或为∞),但当定理条件不满足时,所求极限却不一定不存在,这就是说当两个函数的导数的商的极限不存在时(等于无穷大的情况除外),未定式的极限也可能存在。
说明:
本文内容是老猿学习同济版高数的总结,有需要原教材电子版以及OpenCV、Python基础知识、、图像处理原理介绍相关电子资料,或对文章内有有疑问咨询的,请扫博客首页左边二维码加微信公号,根据加微信公号后的自动回复操作。
更多人工智能数学基础请参考专栏《人工智能数学基础》。
