革新Transformer!清华大学提出全新Autoformer骨干网络,长时序预测达到SOTA
新智元报道
【新智元导读】近日,清华大学软件学院机器学习实验室另辟蹊径,基于随机过程经典理论,提出全新Autoformer架构,包括深度分解架构及全新自相关机制,长序预测性能平均提升38%。
 论文链接:https://arxiv.org/abs/2106.13008
论文链接:https://arxiv.org/abs/2106.13008
研究背景
随着预测时效的延长,直接使用自注意力(self-attention)机制难以从复杂时间模式中找到可靠的时序依赖。
由于自注意力的二次复杂度问题,模型不得不使用其稀疏版本,但会限制信息利用效率,影响预测效果。
深度分解架构:突破将时序分解作为预处理的传统方法,设计序列分解单元以嵌入深度模型,实现渐进式地(progressively)预测,逐步得到可预测性更强的组分。 自相关(Auto-Correlation)机制:基于随机过程理论,丢弃点向(point-wise)连接的自注意力机制,实现序列级(series-wise)连接的自相关机制,且具有的复杂度,打破信息利用瓶颈。 应对长期预测问题,Autoformer在能源、交通、经济、气象、疾病五大领域取得了38%的大幅效果提升。
方法介绍
(1)深度分解架构
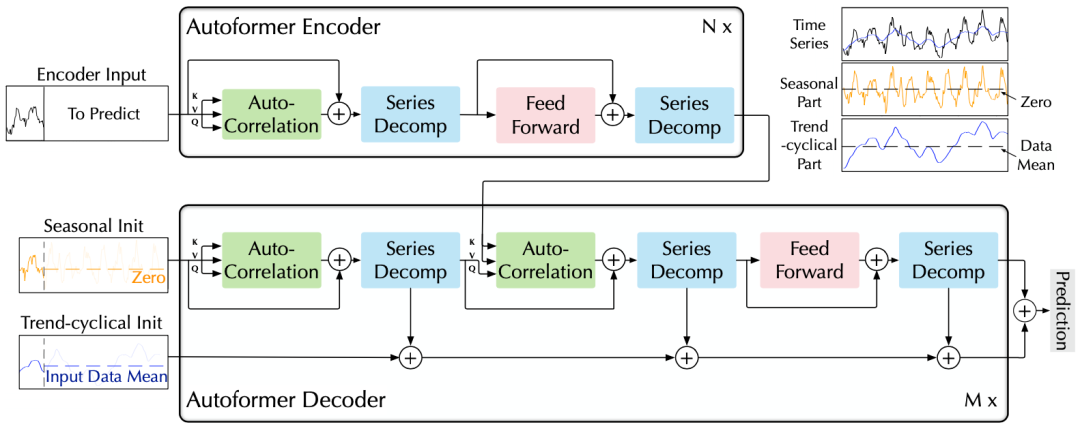
A. 序列分解单元
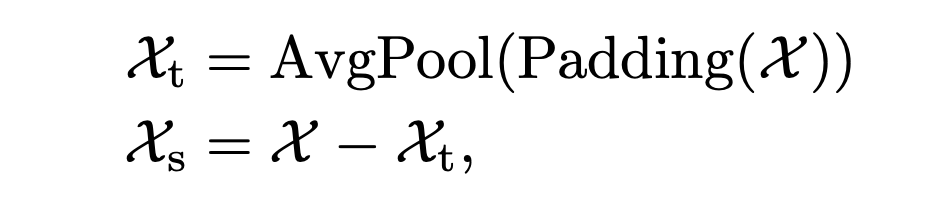
B. 编解码器

对于周期项,使用自相关机制,基于序列的周期性质来进行依赖挖掘,并聚合具有相似过程的子序列; 对于趋势项,使用累积的方式,逐步从预测的隐变量中提取出趋势信息。


A. 基于周期的依赖发现
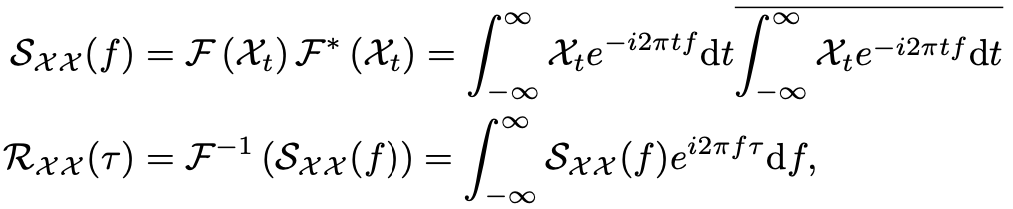
B. 时延信息聚合
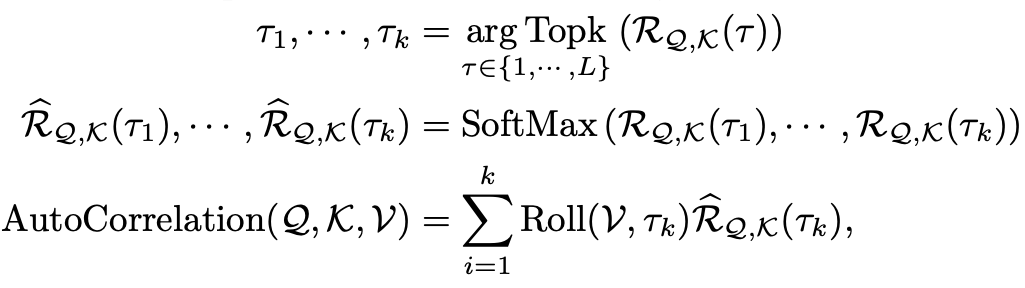
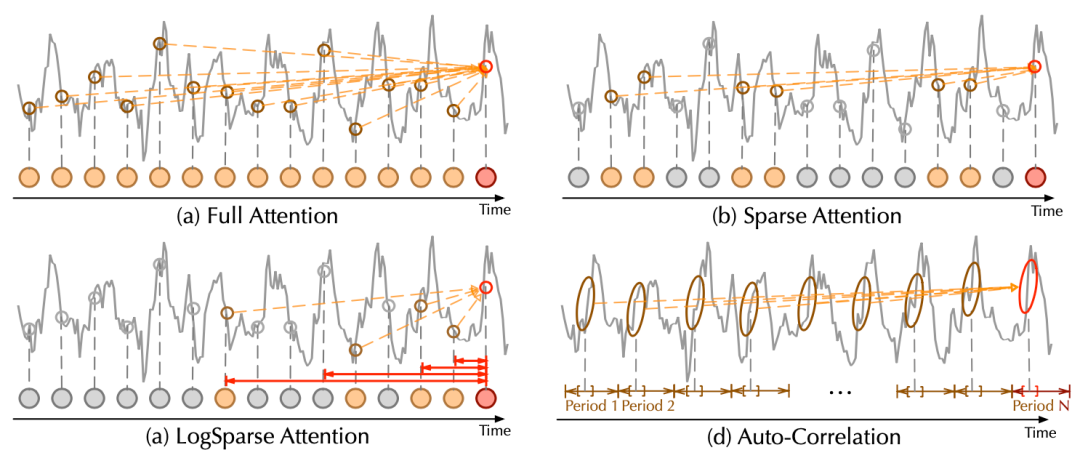
C. 对比分析
实验
(1) 主要结果
 整体实验结果
整体实验结果(2) 对比实验
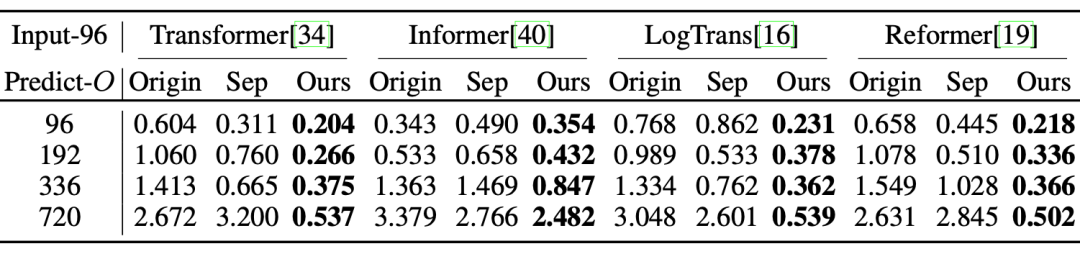

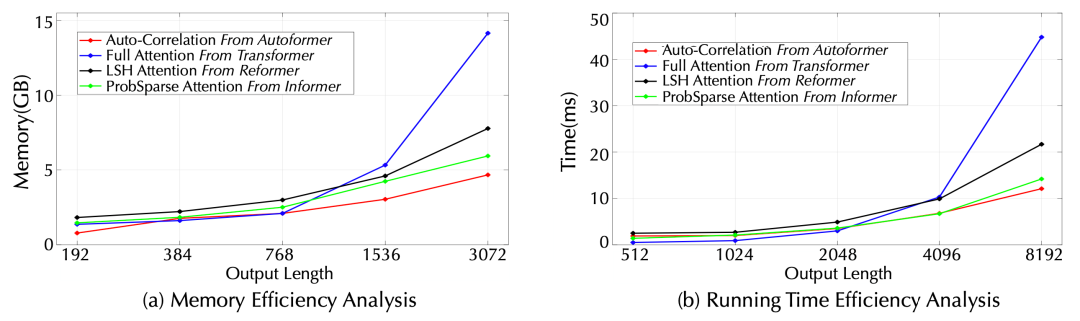
(3) 模型分析
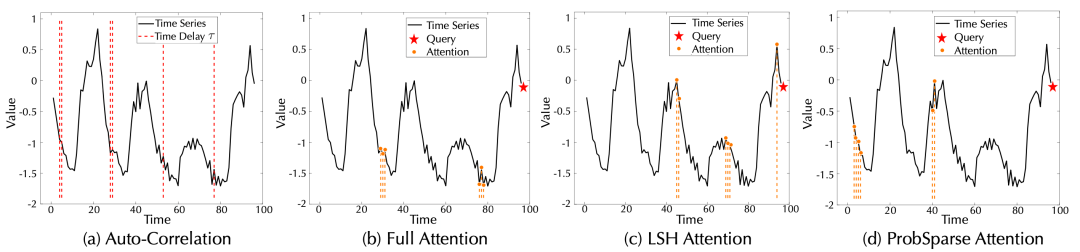
总结

评论
