实战案例|销量预测模型
前言:
这个预测模型比较简单,其实就是统计学,基本大家上学期间都会学到,不过毕业好多年可能也忘了,不妨来复习复习,而且工作中可以实际应用的地方还挺多的。
根据历史月度销量预测2021-09、10、11、12月的销量数据

先看下散点图,大致浏览下是否存在极值(若有,则排除掉)以及两个变量之间是否存在关联趋势

拟合注意事项:
用Excel拟合的时候尽量将各个趋势线均尝试下,选择R²较为接近1的方式。R²越接近1,代表拟合效果越好。
尝试下来,发现多项式拟合效果较好,且“顺序”越往上增加,R²越接近1。但本数据源不多,且多项式拟合多采取二项式或三项式即可满足需求,所以为避免过拟合,取3即可。

拟合出的结果如下,多项式公式如图中所示:

给数据源增加一列辅助列,
将21、22、23、24分别带入y = -0.5908x^3 + 19.576x^2 - 73.697x + 2128.3
则得到2021-09、10、11、12月的预测销量

数据源如下

操作步骤:
➣步骤1:先将月份拉列,销量拉行,制作出折线图。数据源中“月份”是文本格式,需改成日期格式

➣步骤2:点击列上的“月份”,改成离散

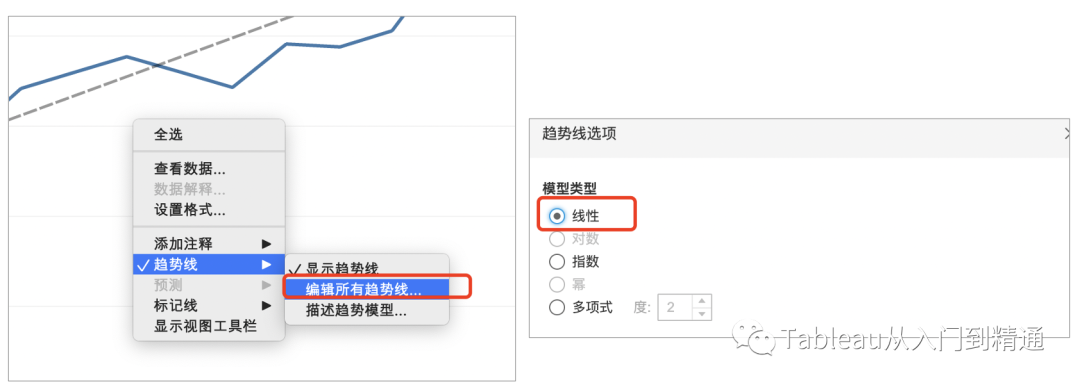
➣步骤3:点击折线图选择“显示趋势线”

点击折线图表,选择“编辑所有趋势线”,可以看到该预测模型为“线性”预测。
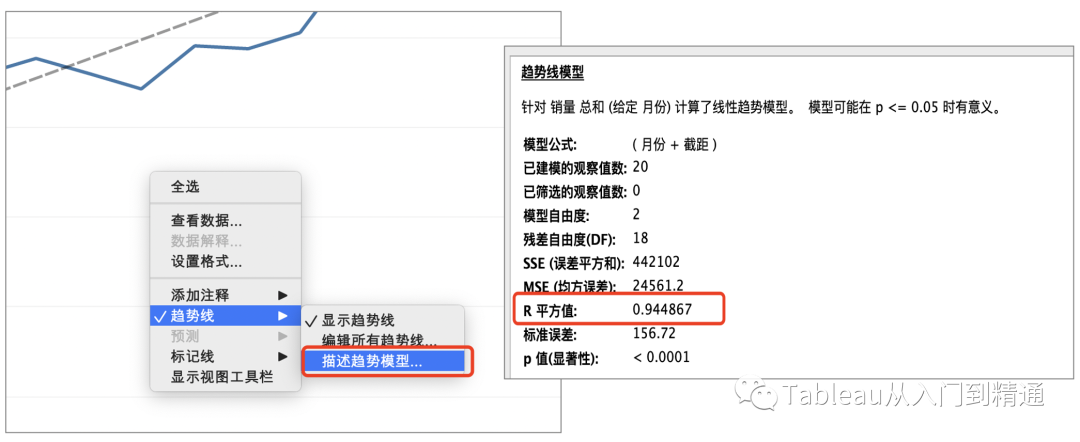
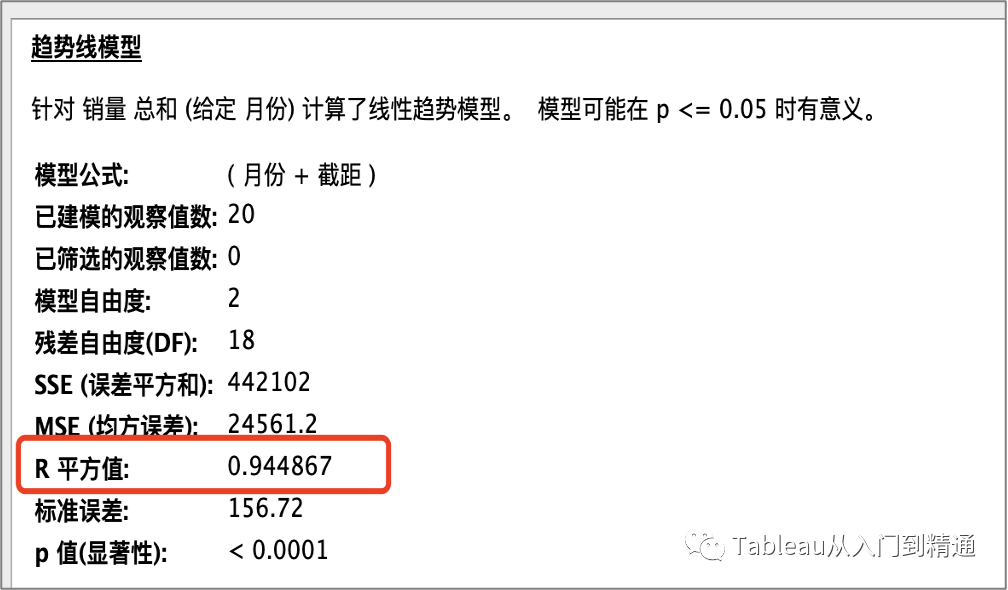
点击折线图表,选择“描述趋势模型”,可以看到该“线性”预测的R平方值
➣步骤4:按照步骤3的方法,选择“编辑所有趋势线”依次选择“线性”、“指数”、“多项式”2度、“多项式”3度,并查看对应的R平方值,选择其中R平方值最靠近1 的模型来作为最终的预测模型。
可以看到:
“线性”预测R方为
“指数”预测R方为

2度“多项式”预测R方为

3度“多项式”预测R方为
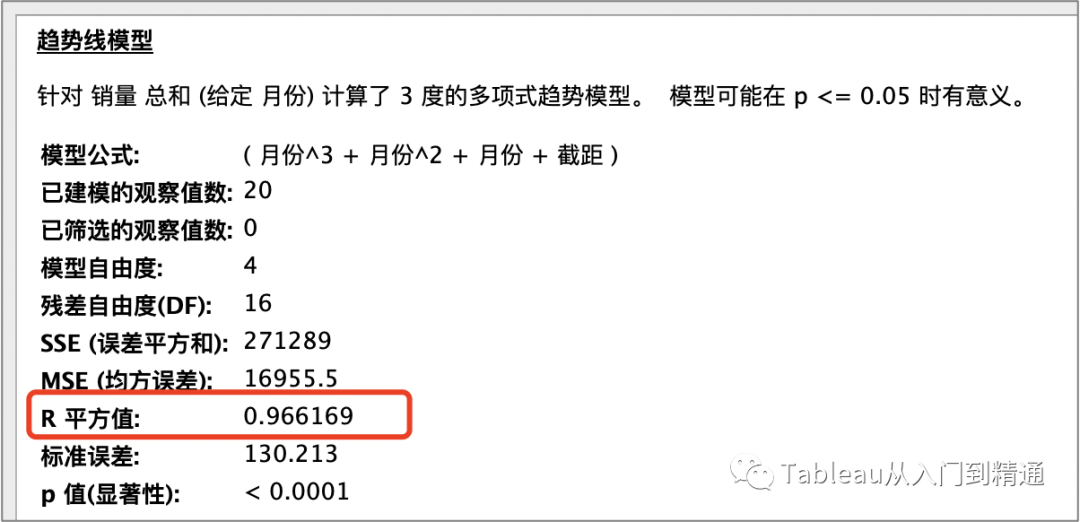
综合对比得出:3度“多项式”预测模型R方更接近1,因此最终采取该预测模型。
➣步骤5:鼠标移动到趋势线上,可以看到拟合公式如下,如案例一中给数据源添加一列辅助列,并将需要预测的月份的辅助列的数字代入公式中,即可得到预测销量。

另外说明:Tableau自带预测功能,但是在本案例中不采用,原因如下:
将月份上的“精确日期”去掉,格式选择月份,点击折线图选择“显示预测”

结果如下图
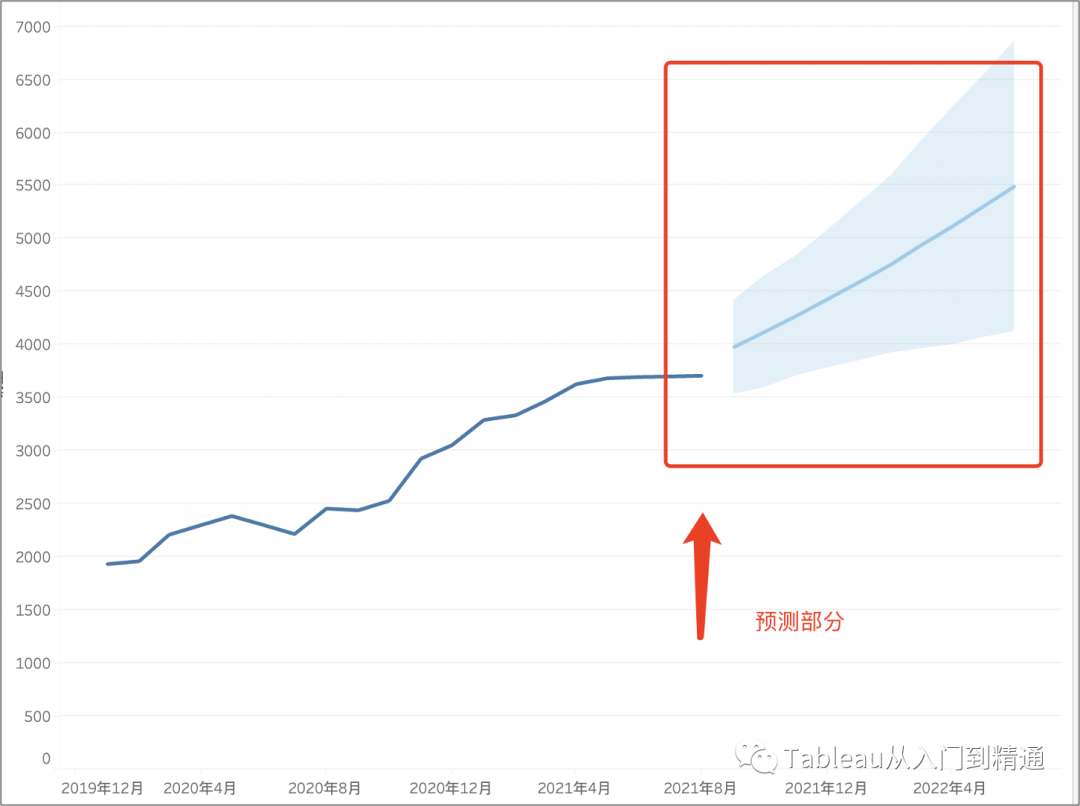
再点击图表选择“预测描述”,可以发现该自动预测模型用的是“指数平滑法”,然而在上述步骤的拟合中发现指数相关预测方法的R方并不是最优。

数据源如下:

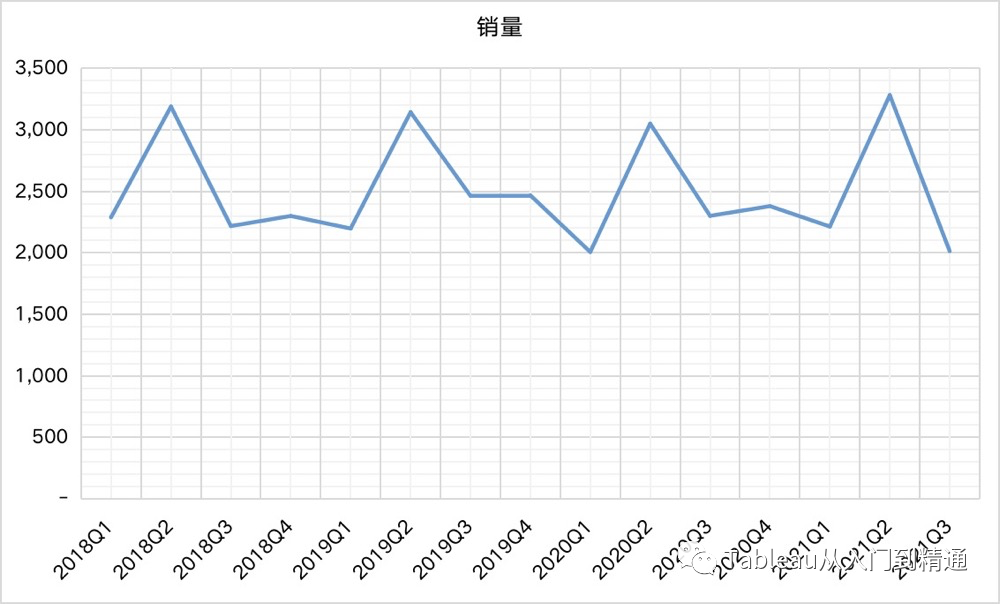
先画出普通折线图,看下是否呈现明显季节性。
下图展示出该销量数据确实呈现季节性,其中第2季度为旺季。则要针对该数据进行去季节化处理。
将数据源通过数据透视表处理成下图所示:
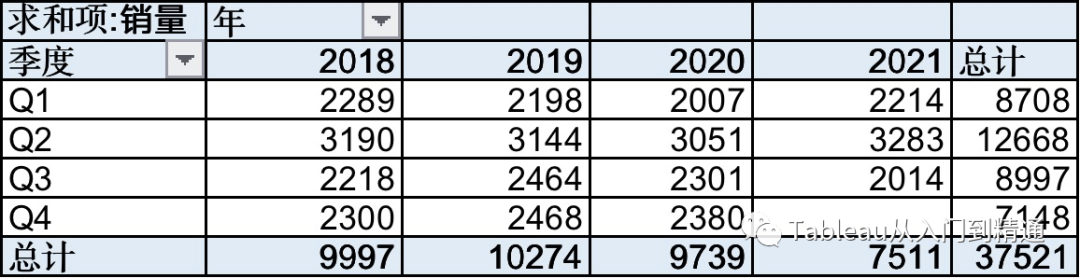
计算每个季度的年度均值,如下图“年平均值”;
计算15个样本的总体平均值,如下图“总平均值”;
用“年平均值”/“总平均值”计算出“季节性指数”

来看一张总结之后的表格
①将计算出的“季节指数”重复添加进下图中的“季节指数”列
②去季节化=销量/季节指数
③根据“辅助列”和“去季节化”后的销量拟合出线性预测公式
y=-2.4907x+2532
之所以拟合线性公式是因为在第②步中已经将季节性因素排除掉了

④将辅助列代入公式,计算出“线性预测”列
⑤将“线性预测”列乘以“季节指数”计算出“季节性调整”列,此列即为最终的预测销量
⑥将“线性预测”列减去“销量”列计算误差,再除以“销量”列计算误差率。
⑦用STDEV()函数选中销量一列,计算出总体标准偏差;
显著性水平参数写为0.05,即置信度是95%;
样本量写15;
用CONFIDENCE()函数计算出置信区间的可浮动值,结果如下截图。
即,有95%的可能性预测值比处于真实值的上下195.92范围内。
可以看到误差都在正常的置信区间内。

⑧将16(辅助列)代入公式,可预测2021Q4的销量。

![[hold住]](https://filescdn.proginn.com/f1e34f24aebe72784fb8ab74353342f5/ea8cfab0e70371fbf7c33d6eceba129f.webp)
![[hold住]](https://filescdn.proginn.com/eb3ac7203d9c4709e75fa4344f93c179/801af8287b005052e868f177987716ed.webp)
![[hold住]](https://filescdn.proginn.com/d4af1d2519706bd6c83b3bf797dcb860/556c4a0f0ae989f8c34acbb45f5444d8.webp)


