最牛损失函数解读: A General and Adaptive Robust Loss Function

极市导读
这篇论文提出了一种自适应的损失函数,并演示了它随着迭代次数的增加,最终找出最佳拟合线的过程。
最近,我看到一篇由Jon Barron在CVPR 2019中提出的关于为机器学习问题开发一个了鲁棒、自适应的损失函数的文章。本文是对 A General and Adaptive Robust Loss Function 一些必要概念的回顾,它还将包含一个简单回归问题上的损失函数的实现。
关于异常值和鲁棒的损失的问题
考虑机器学习问题中最常用的误差之一:均方误差(MSE),它是(y-x)的形式。MSE的一个关键特征是它对大误差的灵敏度比小误差高。用MSE训练的模型将偏向于减少最大的误差。例如,误差为3与与误差为9同等重要。
我使用Scikit-Learn创建了一个例子,以演示在有或没有异常值影响的情况下,模型的拟合是如何在一个简单数据集中变化的。
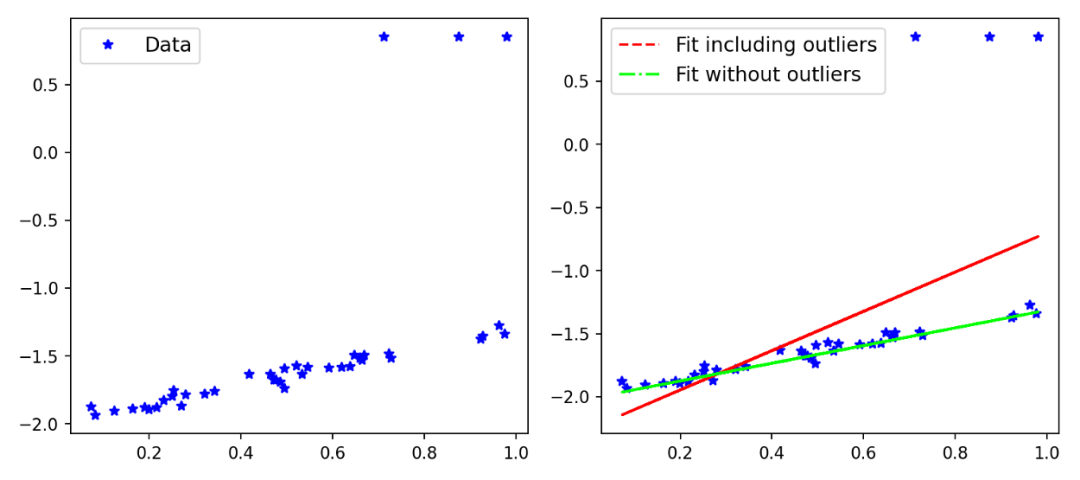
图1::MSE以及离群点的影响
你可以看到的,包含异常值的拟合会受到异常值的影响,但是优化问题应该要求模型受到inliers的影响要大于离群值。当然,在这一点上,你已经可以认为平均绝对误差(MAE)是比MSE更好的选择,因为它对大误差的敏感性较低。有各种类型的稳健性损失(如MAE),对于一个特定的问题,我们可能需要测试各种损失。在训练一个网络的同时,快速测试各种损失函数不是很神奇吗?本文的主要思想是引入一个广义的损失函数,其中损失函数的鲁棒性可以改变,并可以在训练网络的同时训练这个超参数,以提高性能。这比通过执行网格搜索交叉验证来寻找最佳损失所花费的时间要少得多。让我们从下面的定义开始。
鲁棒的以及自适应的损失:一般形式
鲁棒和自适应损失的一般形式如下:
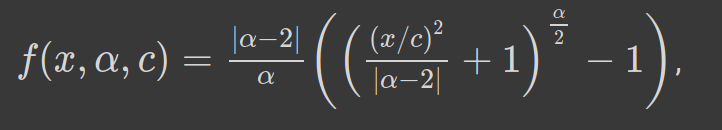
表达式1: 鲁棒的损失: α 是超参数,控制了鲁棒性
α控制损失函数的鲁棒性。c可以看作是一个尺度参数,在x=0附近控制弯曲的尺度。由于α是超参数,我们可以看到,对于α的不同值,损失函数具有相似的形式。让我们看看下面:
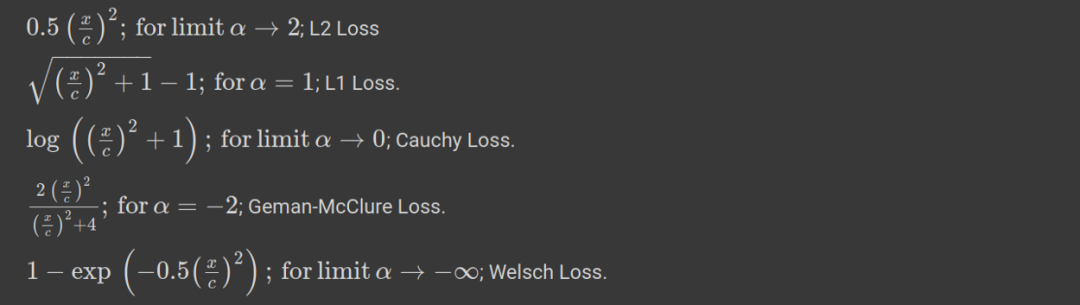
表达式2: 对于不同的α,自适应损失(表达式1)的表现为不同的损失
损失函数在α = 0和2处没有定义,但是取极限我们可以进行近似。从α =2到α =1,损失平稳地从L2损失过渡到L1损失。对于不同的值,我们可以绘制损失函数,看看它如何表现(图2)。
我们也可以花一些时间在这个损失函数的一阶导数上,因为基于梯度的优化需要导数。对于α的不同值,相对于x的导数如下所示。在图2中,我还绘制了不同α的导数和损失函数。

表达式3:鲁棒损失(表达式1)对于不同的α的值相对于x的导数
自适应损失的表现极其导数
下面的图对于理解我们损失的行为是非常重要的。对于下面的图,我已经将尺度参数c固定为1.1。当x = 6.6时,我们可以把它当做x = 6 × c。根据下图,我们可以得出以下关于损失及其导数的推论。
损失函数对x, α和c>0是平滑的,适用于基于梯度的优化。
在原点处损失始终为零,当*|x|>0*时,单调增加。具有单调性损失也可以取对数损失进行比较。
损失相对于α也是单调递增的。这一特性对于损失函数的鲁棒性非常重要,因为我们可以从一个较高的α值开始,然后在优化过程中逐渐(平稳地)减少,从而使鲁棒估计避免局部极小值。
我们看到当|x|<c时,对于不同的α值,导数几乎是线性的。这意味着当它们很小的时候,导数与残差的大小成比例。
对于 α = 2,整个导数与残差的大小成比例。这是一般的MSE (L2)损失的性质。
对于α = 1(L1损失),我们可以看到,在|x|>c之外,导数的幅度饱和到一个恒定值(恰好是1/c)。这意味着残差的影响永远不会超过一个固定的数值。
对于 α < 1导数的大小随|x|>c的变化而减小。这意味着随着残差的增加,它对梯度的影响较小,因此在梯度下降过程中,离群点的影响较小。
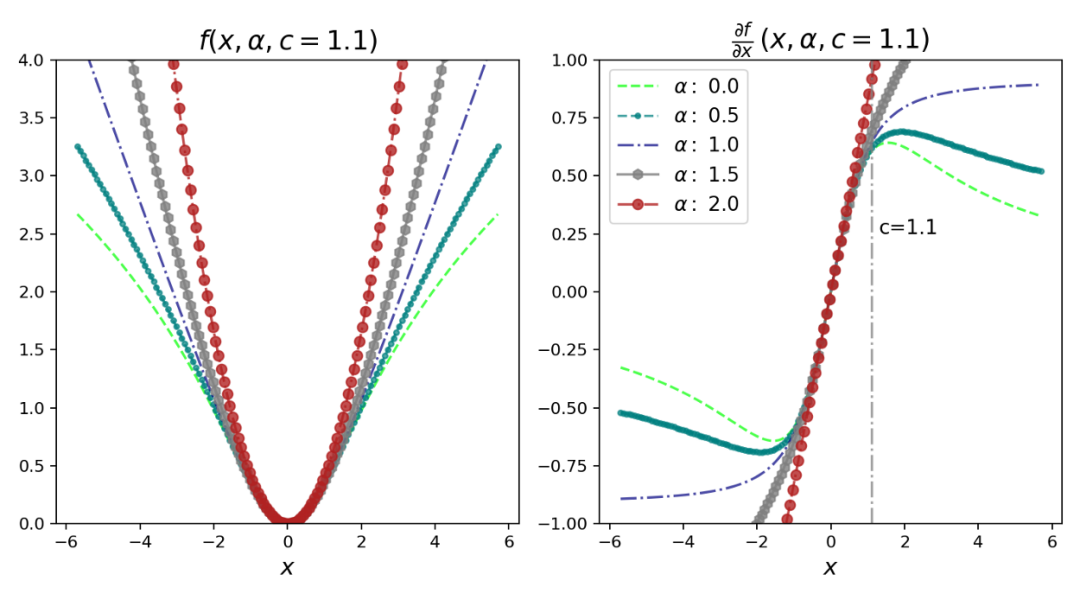
图2:损失函数以及损失函数的梯度,关于α的函数
我还绘制了下面的图,不同α值的鲁棒损失和它的导数的曲面图。
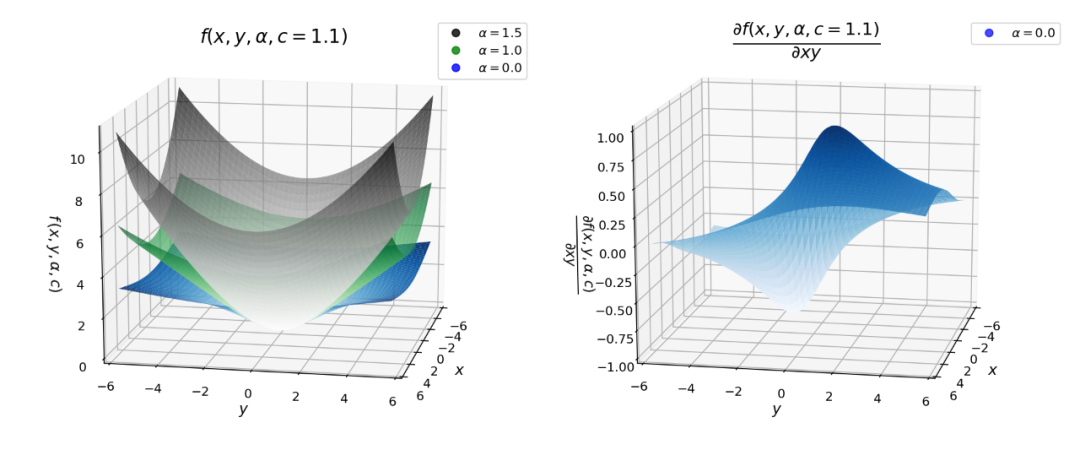
图3:自适应损失函数曲面图(左),其梯度(右)
鲁棒损失的实现:Pytorch和Google Colab
既然我们已经学习了鲁棒和自适应损失函数的基本知识和性质,让我们将其付诸实践。下面使用的代码只是稍微修改了一下Jon Barron 's GitHub存储库中的代码。我还创建了一个动画来描述随着迭代次数的增加,自适应损失如何找到最佳拟合线。
!pip install git+https://github.com/jonbarron/robust_loss_pytorchimport robust_loss_pytorch
我们创建一个简单的线性数据集,包括正态分布的噪声和离群值。因为库使用pytorch,所以我们使用torch将x, y的numpy数组转换为张量。
import numpy as np
import torch
scale_true = 0.7
shift_true = 0.15
x = np.random.uniform(size=n)
y = scale_true * x + shift_true
y = y + np.random.normal(scale=0.025, size=n) # add noise
flip_mask = np.random.uniform(size=n) > 0.9
y = np.where(flip_mask, 0.05 + 0.4 * (1. — np.sign(y — 0.5)), y)
# include outliers
x = torch.Tensor(x)
y = torch.Tensor(y)
接下来我们使用pytorch模块定义一个线性回归类,如下所示:
class RegressionModel(torch.nn.Module):
def __init__(self):
super(RegressionModel, self).__init__()
self.linear = torch.nn.Linear(1, 1)
## applies the linear transformation.
def forward(self, x):
return self.linear(x[:,None])[:,0] # returns the forward pass
接下来,我们对我们的数据拟合一个线性回归模型,但首先使用损失函数的一般形式。在这里,我们使用一个固定的α值(α = 2.0),并且它在整个优化过程中保持不变。正如我们所看到的,对于α = 2.0,损失函数等效于L2损失,而这对于包括异常值在内的问题来说并不是最优的。我们使用学习率为0.01的Adam优化器。
regression = RegressionModel()
params = regression.parameters()
optimizer = torch.optim.Adam(params, lr = 0.01)
for epoch in range(2000):
y_i = regression(x)
# Use general loss to compute MSE, fixed alpha, fixed scale.
loss = torch.mean(robust_loss_pytorch.general.lossfun(
y_i — y, alpha=torch.Tensor([2.]), scale=torch.Tensor([0.1])))
optimizer.zero_grad()
loss.backward()
optimizer.step()
利用鲁棒损失函数的一般形式和固定α值,可以得到拟合直线。图4中绘制了原始数据、真实线(生成数据点时使用的具有相同斜率和偏差的线,排除异常值)和拟合线。
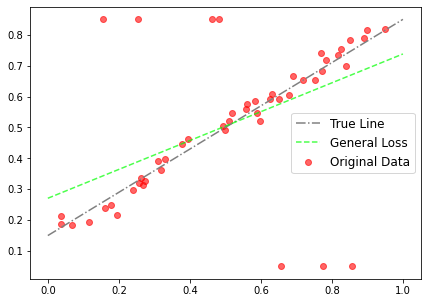
损失函数的一般形式不允许α改变,因此我们必须手工调整 α参数或执行网格搜索。此外,如上图所示,拟合会受到离群值的影响。这是一般情况但是如果我们使用损失函数的适应性版本会发生什么呢?我们调用adaptive loss模块,并初始化α,让它在每个迭代步骤中自适应。
regression = RegressionModel()
adaptive = robust_loss_pytorch.adaptive.AdaptiveLossFunction(
num_dims = 1, float_dtype=np.float32)
params = list(regression.parameters()) + list(adaptive.parameters())
optimizer = torch.optim.Adam(params, lr = 0.01)
for epoch in range(2000):
y_i = regression(x)
loss = torch.mean(adaptive.lossfun((y_i — y)[:,None]))
# (y_i - y)[:, None] # numpy array or tensor
optimizer.zero_grad()
loss.backward()
optimizer.step()
使用这个,以及使用Celluloid模块的一些额外代码,我创建了下面的动画(图5)。在这里,你可以清楚地看到,随着迭代的增加,adaptive loss如何找到最佳拟合线。这个结果接近真实的线,它是可以忽略离群值的影响。
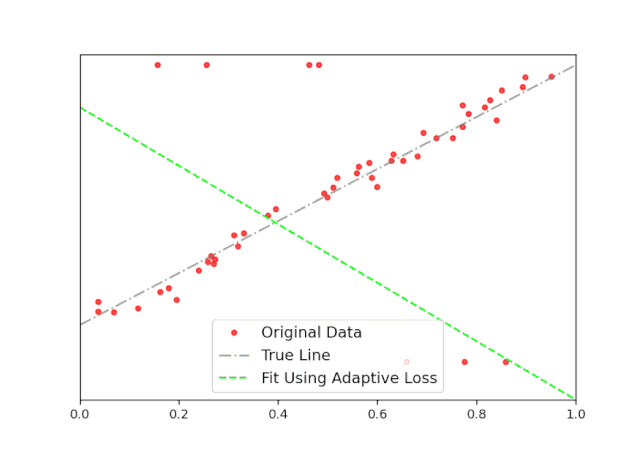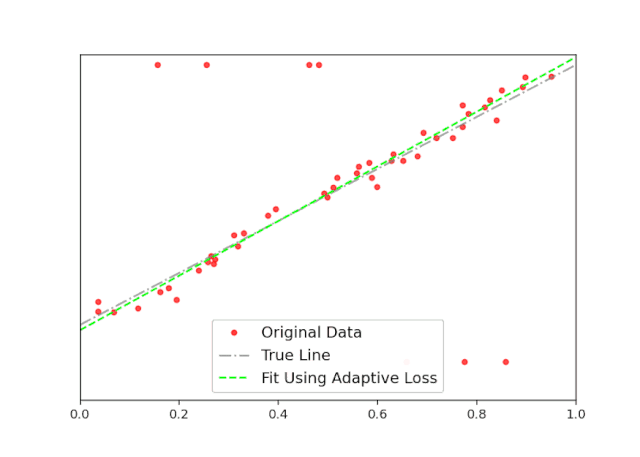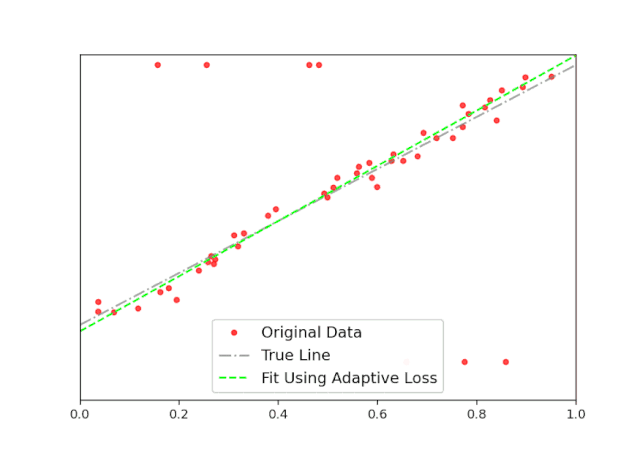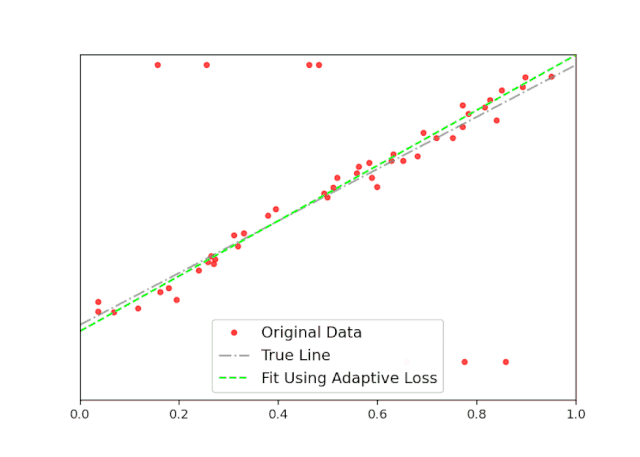
图5:自适应损失函数得到最佳拟合的动画。
讨论
我们已经看到了如何使用包含超参数α的鲁棒损失来动态地寻找最佳损失函数。本文还演示了以α为连续超参数的损失函数的鲁棒性如何被引入到经典的计算机视觉算法中。论文中给出了实现自适应损失的变分自编码器和单目深度估计的例子,这些代码也可以在Jon 's GitHub中找到。但是在这篇论文中,最吸引我的是关于损失函数本身的动机和一步一步的推导。
推荐阅读

