3种时间序列混合建模方法的效果对比和代码实现-轻识

来源：DeepHub IMBA
本文约2700字，建议阅读9分钟
本文中将讨论如何建立一个有效的混合预测器，并对常见混合方式进行对比和分析。

基于树的算法在机器学习生态系统中是众所周知的，它们以主导表格的监督任务而闻名。在学习过程中，树的分裂标准只关注相关特征和有用值的范围，所以给定一组表格特征和要预测的目标，无需太多配置和特定的预处理就可以得到令人满意的结果。

但是基于树和梯度提升模型在时间序列预测领域的表现并不好，很多人更倾向于深度学习的方法。这并不奇怪，因为基于树的模型的弱点在于：在技术上无法推断出比训练数据中更高/更低的特征值。他们几乎不可能预测所见区间之外的值。相反，经典的线性回归可能较少受到数据动态行为的影响。既然线性回归擅长推断趋势，而梯度提升擅长学习交互，是否可以将它们结合起来呢？本文目标是创建“混合”预测器，结合互补的学习算法，让一个的优势弥补另一个的弱点。

在使用深度学习时，更容易想到“混合模型”，因为神经网络的无限架构组合和个性化训练过程在定制方面提供了巨大的好处。使用树模型开发定制的混合是比较麻烦的。linear-tree，这个 python 包是一个不错的选择，它提供混合模型架构，混合了基于树的模型和线性模型的学习能力。不仅如此，LGBM 或 XGBoost 也引入了用树叶中的线性近似拟合梯度提升的能力。

在这篇文章中，我尝试从头开始构建一个混合预测器。下面需要做的就是按照两步的方法来学习系统模式。

基础知识

为了设计有效的混合，我们需要对时间序列的构建方式有一个大致的了解。时间序列一般可以通过将三个组成部分（趋势、季节和周期）加上一个本质上不可预测的项（误差）加在一起来精确描述。

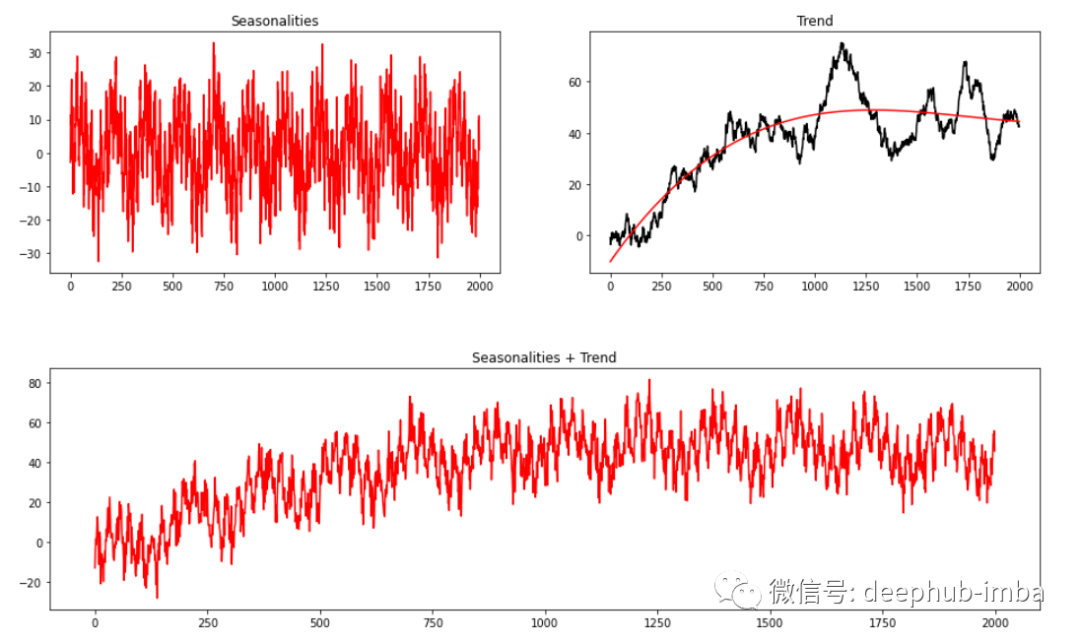
series = trend + seasons + cycles + error

学习时间序列组件可以看作是一个迭代过程：

首先，学习趋势并将其从原始序列中减去，得到残差序列；
其次，从去趋势的残差中学习季节性并减去季节；
最后，学习周期并减去周期。

换句话说，我们使用一种算法来拟合特定的组件序列，然后使用另一种算法来拟合残差序列。最终的预测是各种模型组件的预测相加。

为了尝试构建混合模型，我们开始生成一些具有双季节性模式和趋势分量的时间序列数据。

np.random.seed(1234)seas1 = gen_sinusoidal(timesteps=timesteps, amp=10, freq=24, noise=4)seas2 = gen_sinusoidal(timesteps=timesteps, amp=10, freq=24*7, noise=4)
rw = gen_randomwalk(timesteps=timesteps, noise=1)X = np.linspace(0,10, timesteps).reshape(-1,1)X = np.power(X, [1,2,3])m = LinearRegression()trend = m.fit(X, rw).predict(X)
plt.figure(figsize=(16,4))plt.subplot(121)plt.plot(seas1 + seas2, c='red'); plt.title('Seasonalities')plt.subplot(122)plt.plot(rw, c='black'); plt.plot(trend, c='red'); plt.title('Trend')
plt.figure(figsize=(16,4))plt.plot(seas1 + seas2 + trend, c='red'); plt.title('Seasonalities + Trend')

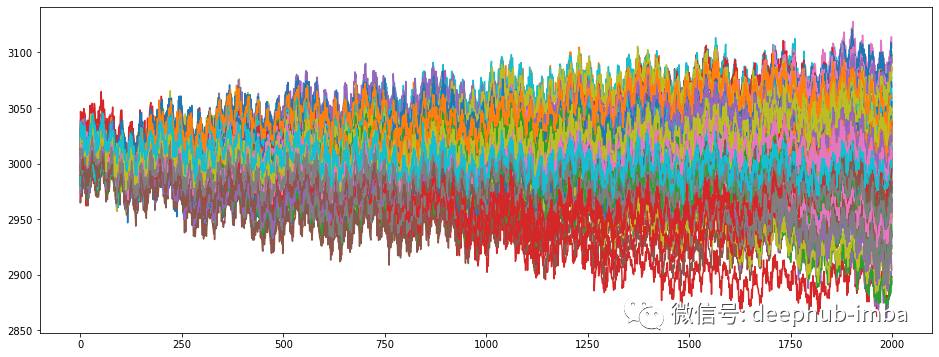
在随机游走序列上拟合三次多项式可以获得未知趋势。结果是一条平滑的趋势线，它被添加到季节性分量中以获得最终的时间序列。可以通过以这种方式生成多个时间序列，并尝试预测它们对各种解决方案进行基准测试。


df.plot(legend=False, figsize=(16,6))

实验方法

本文中尝试了四种不同的方法：

拟合一个简单的线性模型；
differencing：使用差分变换，使目标变得稳定；
hybrid additive：拟合具有最优的线性模型推断趋势。然后用梯度提升对去趋势序列进行建模；
hybrid inclusive.：拟合梯度提升，包括外推趋势（获得拟合具有最优线性模型拟合的趋势）作为特征。

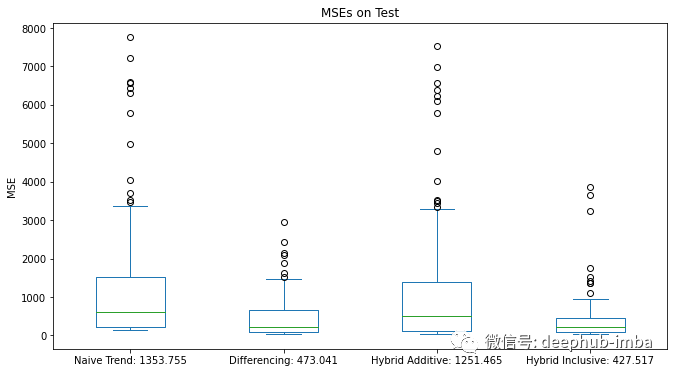
除了最基本的解决方案，上面的所有方法都使用一些样条变换作为特征。这些特征可以很好地捕捉了季节性模式。通过在训练数据上搜索最佳线性模型来计算最佳趋势。使用时间交叉验证策略搜索一些最佳参数配置。

结果

对于可以使用的每个系列，都尝试了上面所有提到的方法，并将结果存储在测试数据上。

### 训练过程略，请查看最后的完整源代码 ###
scores = pd.DataFrame({  f'{score_naive}': mse_naive,  f'{score_diff}': mse_diff,  f'{score_hybrid_add}': mse_hybrid_add,  f'{score_hybrid_incl}': mse_hybrid_incl})
scores.plot.box(figsize=(11,6), title='MSEs on Test', ylabel='MSE')

hybrid inclusive 获得最低的平均测试误差，其次是差分法。hybrid additive的表现低于我们的预期，因为它的错误几乎是差分方法的三倍。一般来说，在对动态系统（例如本文的实验中提出的系统）进行建模时，对目标值进行差分操作是一个很好的选择。混合方法之间的巨大性能差异也表现出了一些问题。让我们检查一下下结果，看看会发生什么。

c = 'ts_11'
df[c].plot(figsize=(16,6), label='true', alpha=0.3, c='black')
df_diff[c].plot(figsize=(16,6), label='differencing pred', c='magenta')df_hybrid_add[c].plot(figsize=(16,6), label='hybrid addictive pred', c='red')df_hybrid_incl[c].plot(figsize=(16,6), label='hybrid inclusive pred', c='blue')df_naive[c].plot(figsize=(16,6), label='trend pred', c='lime', linewidth=3)
plt.xlim(0, timesteps)plt.axvspan(0, timesteps-test_mask.sum(), alpha=0.2, color='orange', label='TRAIN')plt.axvspan(timesteps-test_mask.sum(), timesteps, alpha=0.2, color='green', label='TEST')plt.legend()

预测比较1

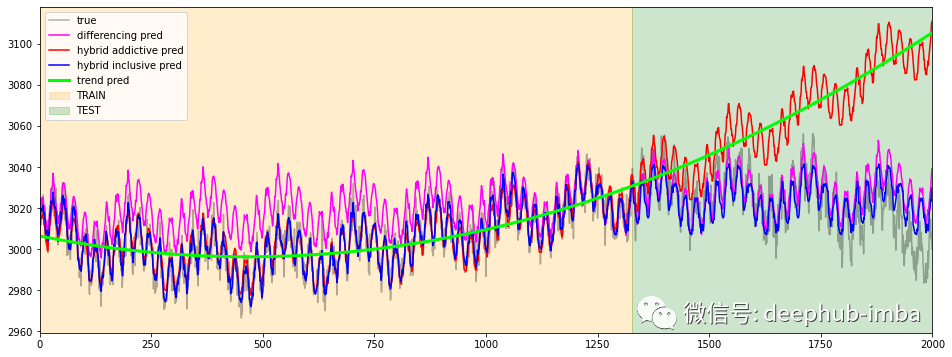
c = 'ts_33'
df[c].plot(figsize=(16,6), label='true', alpha=0.3, c='black')
df_diff[c].plot(figsize=(16,6), label='differencing pred', c='magenta')df_hybrid_add[c].plot(figsize=(16,6), label='hybrid addictive pred', c='red')df_hybrid_incl[c].plot(figsize=(16,6), label='hybrid inclusive pred', c='blue')df_naive[c].plot(figsize=(16,6), label='trend pred', c='lime', linewidth=3)
plt.xlim(0, timesteps)plt.axvspan(0, timesteps-test_mask.sum(), alpha=0.2, color='orange', label='TRAIN')plt.axvspan(timesteps-test_mask.sum(), timesteps, alpha=0.2, color='green', label='TEST')plt.legend()

预测比较2

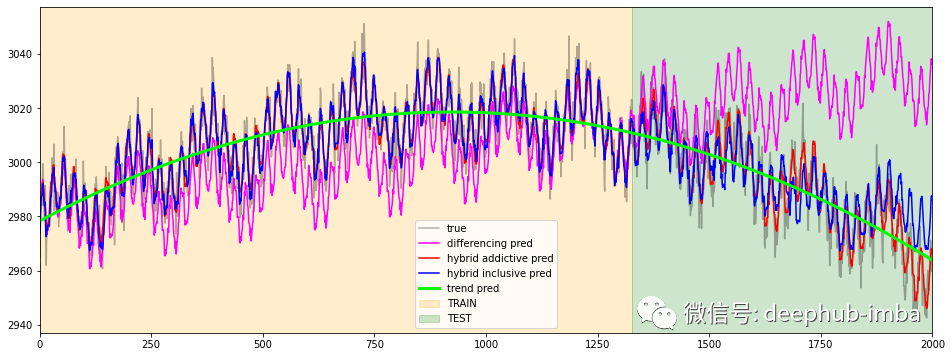
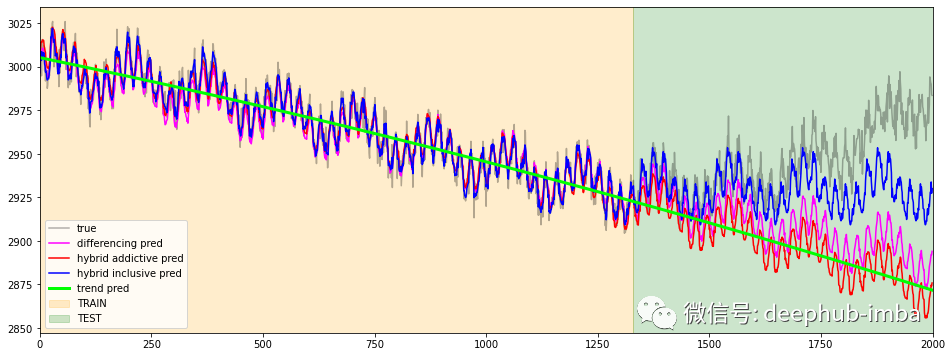
c = 'ts_73'
df[c].plot(figsize=(16,6), label='true', alpha=0.3, c='black')
df_diff[c].plot(figsize=(16,6), label='differencing pred', c='magenta')df_hybrid_add[c].plot(figsize=(16,6), label='hybrid addictive pred', c='red')df_hybrid_incl[c].plot(figsize=(16,6), label='hybrid inclusive pred', c='blue')df_naive[c].plot(figsize=(16,6), label='trend pred', c='lime', linewidth=3)
plt.xlim(0, timesteps)plt.axvspan(0, timesteps-test_mask.sum(), alpha=0.2, color='orange', label='TRAIN')plt.axvspan(timesteps-test_mask.sum(), timesteps, alpha=0.2, color='green', label='TEST')plt.legend()

预测比较3

从上面的一堆图像中，可以更好地理解additive 方法的“失败”。它的表现与之前趋势拟合的好坏密切相关。如果趋势估计不准确，那么最终预测将更不准确。但这种行为通过hybrid inclusive方法得到缓解，因为趋势作为特征包含在模型中。因此梯度提升可以纠正/减轻最终的预测误差。

总结

在这篇文章中，介绍了建立时间序列混合预测模型的不同方法。需要强调的重要一点是，除了这里展示的方法外，还有许多方法可以组合机器学习模型。如果我们能清楚理解标准算法是如何工作的，便能够更轻松地调试或理解混合创造的可能缺陷或缺陷。

最后，本文的完整代码在这里：

https://github.com/cerlymarco/MEDIUM_NoteBook/tree/master/Hybrid_Trees_Forecasting

作者：Marco Cerliani

编辑：黄继彦