每日一道 LeetCode (48):最长回文子串

❝每天 3 分钟,走上算法的逆袭之路。
❞
前文合集
代码仓库
GitHub:https://github.com/meteor1993/LeetCode
Gitee:https://gitee.com/inwsy/LeetCode
题目:最长回文子串
难度:「中等」
题目来源:https://leetcode-cn.com/problems/longest-palindromic-substring/
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2:
输入: "cbbd"
输出: "bb"
解题方案一:暴力解法
暴力方案就很适合我这种脑子不够用的人,首先把字符串中的所有子串取出来,当然哈,取长度大于 1 的子串,不然也没啥意义。
然后挨个判断取出来的子串是否回文串,判断完了以后取到最大的那个,然后返回出来,结束。
public String longestPalindrome(String s) {
int len = s.length();
if (len < 2) {
return s;
}
// 先把字符串转成数组
char[] charArray = s.toCharArray();
// 定义初始位置
int left = 0;
// 定义字符串长度
int length = 1;
// 获取所有子串
for (int i = 0; i < len - 1; i++) {
for (int j = i + 1; j < len; j++) {
if (j - i + 1 > length && valid(charArray, i, j)) {
left = i;
length = j - i + 1;
}
}
}
return s.substring(left, left + length);
}
// 判断是否回文串
private boolean valid(char[] charArray, int left, int right) {
while (left < right) {
if (charArray[left] != charArray[right]) {
return false;
}
left++;
right--;
}
return true;
}
这个答案慢肯定是慢,时间复杂度达到了 O(n^3) ,不慢才有鬼了。
解题方案二:中心扩散
上面的方案是从两边开始往中间夹,中心扩散的思想是从中间开始往两边进行扩散。
我在答案中找到了一个非常形象的图解,和大家分享一下:
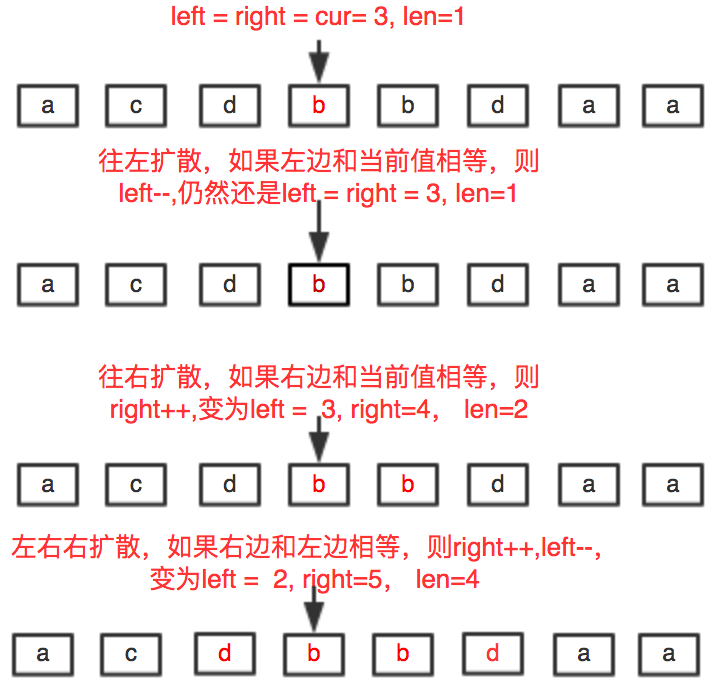
解释一下这张图,现在假设有一个字符串 「acdbbdaa」 ,从第一个 b 位置开始找最长回文串。
- 首先往左寻找与当期位置相同的字符,直到遇到不相等为止。
- 然后往右寻找与当期位置相同的字符,直到遇到不相等为止。
- 最后左右双向扩散,直到左和右不相等。
这时我们找到了从 b 开始最长的回文子串,然后在程序中记录下来。
每一个位置开始都按这个方案去找最长的回文子串,最后得到的结果就是最长的回文子串。
public String longestPalindrome_1(String s) {
if (s == null || s.length() == 0) return "";
int length = s.length();
// 定义左右指针
int left = 0, right = 0;
// 定义长度
int len = 1;
// 定义最大开始位置和最长子串长度
int maxStart = 0, maxLen = 0;
for (int i = 0; i < length; i++) {
left = i - 1;
right = i + 1;
// 计算左边
while (left >= 0 && s.charAt(left) == s.charAt(i)) {
len++;
left--;
}
// 计算右边
while (right < length && s.charAt(right) == s.charAt(i)) {
len++;
right++;
}
// 两边一起扩散
while (left >= 0 && right < length && s.charAt(left) == s.charAt(right)) {
len += 2;
left--;
right++;
}
// 如果当前长度大于最大长度
if (len > maxLen) {
maxLen = len;
maxStart = left;
}
// 下次循环前重置 len
len = 1;
}
return s.substring(maxStart + 1, maxStart + 1 + maxLen);
}
解题方案三:动态规划
动态规划我的理解实际上就是一个把已经判断过的信息缓存起来的一种方案,很像我们在做 Web 开发的时候用到的 redis ,只是在答案中换成了一个矩阵或者说是二维数组。
如果一个字符串 s[l, r] 是一个回文串,那么 s[l + 1, r - 1] 一定也是一个回文串,相当于两头各去掉一个字符。
如果这时我们直接通过某种方式直接可以知道 s[l + 1, r - 1] 是一个回文串,那么只需要判断 s[i] 和 s[j] 相等就可以了。
所以就有了下面的代码:
public String longestPalindrome_2(String s) {
if (s == null || s.length() == 0) return s;
int length = s.length();
int maxStart = 0; //最长回文串的起点
int maxEnd = 0; //最长回文串的终点
int maxLen = 1; //最长回文串的长度
// 定义一个布尔矩阵
boolean[][] dp = new boolean[length][length];
for (int r = 1; r < length; r++) {
for (int l = 0; l < r; l++) {
if (s.charAt(r) == s.charAt(l) && (r - l <= 2 || dp[l + 1][r - 1] == true)) {
dp[l][r] = true;
if (r - l + 1 > maxLen) {
maxLen = r - l + 1;
maxStart = l;
maxEnd = r;
}
}
}
}
return s.substring(maxStart, maxEnd + 1);
}
可以看到耗时也是蛮多的。
答案中还给出了一种叫做 Manacher 算法的方案,原谅我比较菜,属实是没看懂,就不拿出来献丑了。

