从零实现深度学习框架(三)计算图运算补充

引言
本着“凡我不能创造的,我就不能理解”的思想,本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架,该框架类似PyTorch能实现自动求导。
要深入理解深度学习,从零开始创建的经验非常重要,从自己可以理解的角度出发,尽量不适用外部完备的框架前提下,实现我们想要的模型。本系列文章的宗旨就是通过这样的过程,让大家切实掌握深度学习底层实现,而不是仅做一个调包侠。
本文额外介绍一些操作的计算图,像求最大值(Max)、切片(Slice)、变形(Reshape)和转置(Transpose)。
Max
Max操作要复杂一些,我们先来看一下当输入是一个1D数组时:
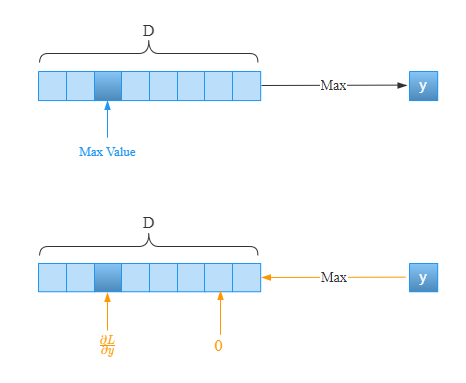
取1D数组中,假设第三个元素为最大值,那么经过Max操作后,返回的就是这个元素。当反向传播时,只有第三个元素有梯度,其他元素的梯度为。此时只有在第三个元素处才会将上游的梯度原封不动的传给下游,其他元素处将不会有梯度往下游传递。就像电路中的开关一样,只有第三个元素处开关是打开的,有电流通过;其他元素的位置的开关是关闭的,没有电流通过。下面通过代码演示一下:
> import torch
# 随机生成一个(8,)的一维数组
> x = torch.randint(10, (8,), dtype=torch.float, requires_grad=True)
> print(x) # 第三个元素为最大值
tensor([3., 1., 8., 0., 0., 3., 6., 4.], requires_grad=True)
> y = torch.max(x)
> print(y)
tensor(8., grad_fn=)
> y.backward()
> print(x.grad) # 只有第三个元素才有梯度
tensor([0., 0., 1., 0., 0., 0., 0., 0.])
我们再来看输入是2D的情况:

在2D数组中,如果是沿着行的方向,即axis=0时,取每列的最大值,如果保持维度的话,就变成了一个的数组。就是上图蓝色背景对应的元素。在反向传播时,只有这些元素才会将上游的梯度传递到下游,其他元素的位置不会有梯度往下游传递。
通过代码来演示一下:
> D, N = 5, 4
> x = torch.randint(10,(N,D), dtype=torch.float, requires_grad=True)
> print(x)
tensor([[1., 1., 5., 9., 1.],
[4., 5., 9., 8., 7.],
[1., 1., 7., 7., 9.],
[8., 1., 1., 0., 7.]], requires_grad=True)
> y = torch.max(x, dim=0, keepdim=True).values
> print(y)
tensor([[8., 5., 9., 9., 9.]], grad_fn=)
> y.sum().backward() # 或者y.backward([[1., 1., 1., 1., 1.]])
> print(x.grad)
tensor([[0., 0., 0., 1., 0.],
[0., 1., 1., 0., 0.],
[0., 0., 0., 0., 1.],
[1., 0., 0., 0., 0.]])
有一点值得注意的是,假设我们取最大值时,包含重复元素,会怎样呢?
给个极端的例子:
# 极端的例子
> x = torch.ones((2,5), dtype=torch.float, requires_grad=True)
> x
tensor([[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]], requires_grad=True)
> y = torch.max(x)
> y.backward()
> x.grad
tensor([[0.1000, 0.1000, 0.1000, 0.1000, 0.1000],
[0.1000, 0.1000, 0.1000, 0.1000, 0.1000]])
在这个例子中,共有10个元素,形状是。元素值都是相等的,如果直接调用torch.max,在反向传播后,梯度被这些元素给均分了,其实也很好理解。毕竟又不是复制操作。
当我们指定维度的时候,还会这样吗?
# 极端的例子
> x = torch.ones((2,5), dtype=torch.float, requires_grad=True)
> x
tensor([[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]], requires_grad=True)
> y = torch.max(x, axis=0) # 指定axis=0,取每列的最大值
> y
torch.return_types.max(values=tensor([1., 1., 1., 1., 1.], grad_fn=), indices=tensor([0, 0, 0, 0, 0])) # 每列的最大值都是1,但是仅记录了遇到的第一个元素索引
> y.values.sum().backward()
> print(x.grad)
tensor([[1., 1., 1., 1., 1.],
[0., 0., 0., 0., 0.]])
此时,PyTorch中的表现是这样的。取每列的最大值,每列都有一个梯度,但是遇到重复元素的时候,并没有把上游传过来的梯度进行平分。博主更倾向于会均分梯度,因此在我们实现的时候,会考虑这一点。
Slice
切片(Slice)也是一种常见的操作,比如我们从数组中取出某个元素、某一列、某一行等。我们已经了解了Max操作反向传播的原理。那么理解切片应该也不难。只有选中的元素才有资格传递梯度到下游。
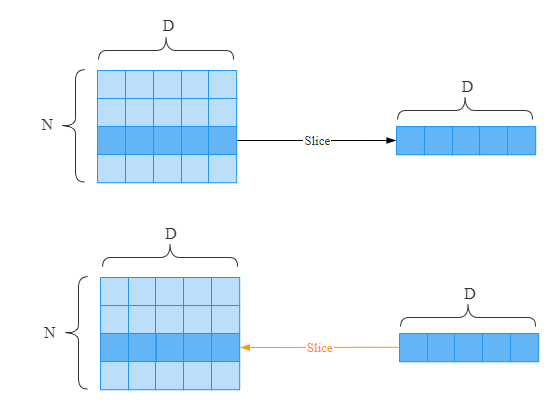
在上面这个的数组中,假设通过切片选择了第三行,那么反向传播时,只有第三行的元素上才有梯度往下游传递。通过代码描述如下:
> D, N = 5, 4
> x = torch.randint(10, (N,D), dtype=torch.float, requires_grad=True)
> x
tensor([[3., 8., 8., 4., 0.],
[0., 5., 6., 9., 6.],
[6., 8., 8., 1., 8.],
[2., 1., 8., 7., 5.]], requires_grad=True)
> y = x[2,:] # 取第2行
> y
tensor([6., 8., 8., 1., 8.], grad_fn=)
> y.sum().backward()
> x.grad
tensor([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[1., 1., 1., 1., 1.],
[0., 0., 0., 0., 0.]])
Reshape
变形(Reshape)操作的反向传播其实是最简单的。假设经过y = x.reshape(..),在反向传播时,只要保证梯度的形状和x保持一致即可。
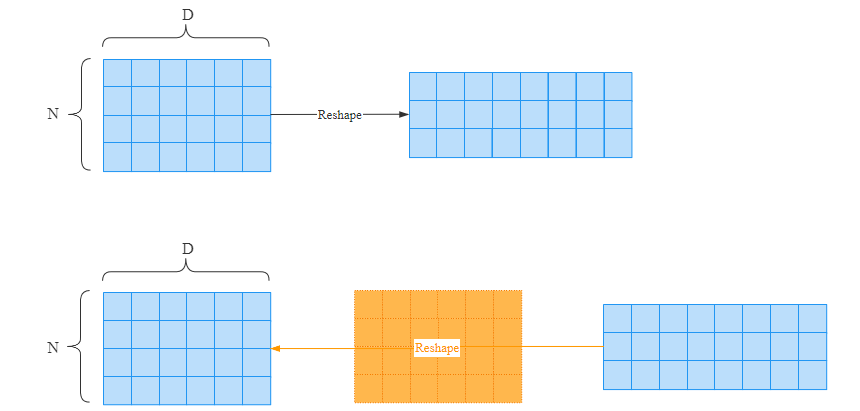
我们通过代码来验证一下:
> D, N = 6, 4
> x = torch.randint(10, (N,D), dtype=torch.float, requires_grad=True)
> x # (4,6)的数组
tensor([[9., 4., 8., 7., 6., 0.],
[7., 4., 2., 9., 4., 4.],
[7., 1., 8., 2., 4., 7.],
[8., 8., 9., 2., 6., 6.]], requires_grad=True)
> y = x.reshape(3, 8) # (4,6) -> (3,8)
> y
tensor([[9., 4., 8., 7., 6., 0., 7., 4.],
[2., 9., 4., 4., 7., 1., 8., 2.],
[4., 7., 8., 8., 9., 2., 6., 6.]], grad_fn=)
> y.sum().backward()
> x.grad
tensor([[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.]])
Transpose
转置(Transpose,我司CV大佬称为旋转)和Reshape类似,所有元素的梯度都会往下游传递。但是转置和Reshape操作本身又是有很大不同的。我们先来看一下它们的区别。
> import matplotlib.pyplot as plt
> import matplotlib.image as mpimg
> import numpy as np
> img_array = mpimg.imread('https://gitee.com/nlp-greyfoss/images/raw/master/data/20211217174850.png')
> plt.imshow(img_array) # 显示图片
> plt.axis("off")
> img_array.shape
(157, 210, 3)

该图片的形状为:
宽: 210 像素 高: 157 像素 RGB: 3
假设我们想对图片进行旋转,先通过Reshape进行,保持最后一个维度不变,以能展示出图片。
> reshaped = img_array.reshape((210,157,3))
> plt.imshow(reshaped)
> plt.axis("off")
> reshaped.shape
(210, 157, 3)

虽然图片是可以显示出来,但是图片变成了很多条状的东西。我们可以通过下图理解Reshape做了什么事情:

Reshape改变矩阵形状后,里面的元素还是根据原来的顺序依次排列的。这会导致这些像素的相对位置会发生变化。
我们再进行Transpose操作。
> transposed = img_array.transpose((1,0,2)) # 交换第0和第1个维度: (0,1,2) -> (1,0,2)
> plt.imshow(transposed)
> plt.axis("off")

可以看到,Transpose并不会改变元素的相对位置。具体如下:

Transpose对于矩阵来说,就是转置,也可以理解为对图像进行旋转。
转置的计算图就不画了,经过上面的探讨应该能很好地理解。我们来看一下转置操作如何进行反向传播。
> x = torch.Tensor(np.arange(24).reshape(2,3,4))
> x.requires_grad = True
> print(x.shape)
> print(x)
torch.Size([2, 3, 4])
tensor([[[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]],
[[12., 13., 14., 15.],
[16., 17., 18., 19.],
[20., 21., 22., 23.]]], requires_grad=True)
> axis = (0,1,2) # 和原来的轴保持一致,演示不转置的结果
> y = torch.permute(x,axis) # torch中的转置
> y.sum().backward()
> x.grad
tensor([[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]],
[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]]])
> x.grad.shape
torch.Size([2, 3, 4])
可以看到,果然和Reshape一样,哪怕做了个假转置,也会有梯度。而且梯度的维度和x一致。
所以,在反向传播的时候,我们要将上游传递过来的梯度,进行逆Reshape操作,保证和x的维度一致。
我们创建一个维度的向量。
> a = np.arange(24).reshape(2,3,4)
> a
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
下面我们先对其进行转置,然后探讨一下如何把转置后的结果,转置回来。
> b = a.transpose(2,0,1)
> print(b.shape) #(0,1,2) -> (2,0,1) : 得到(4,2,3) 即第0轴到了中间,第1轴到了最后,第2轴到了最前面。
> print(b)
(4, 2, 3)
[[[ 0 4 8]
[12 16 20]]
[[ 1 5 9]
[13 17 21]]
[[ 2 6 10]
[14 18 22]]
[[ 3 7 11]
[15 19 23]]]
由。所以要转置回来,我们需要把进行一个怎么样的转置,才会变回来?中括号里面的数字表示现在对应的轴。所以我们应该把对应的轴交换到最后(2轴),把对应的轴交换到中间(1)轴,把轴交换到最前(0轴)。我们要对当前的进行一个这样的转置操作:b.reshape(1,2,0)。下面来验证看:
> b.transpose(1,2,0)
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
看起来不错,但是每次这么分析,很耗时间啊。这里这有3个维度,如果有5个维度怎么办,有什么规律吗?
嘿,还确实有规律,就是对a转置时的元组(或者说是轴列表)进行argsort(对元素按从小到大进行排序,但返回的是排序后的索引)
我们来试一下:
> b.transpose(np.argsort((2,0,1)))
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
总结
至此,我们经常用到操作的计算图都了解完毕了,下篇文章开始通过Python实现这些计算图来创造一个我们自己的自动求导工具。
最后一句:BUG,走你!


Markdown笔记神器Typora配置Gitee图床
不会真有人觉得聊天机器人难吧(一)
Spring Cloud学习笔记(一)
没有人比我更懂Spring Boot(一)
入门人工智能必备的线性代数基础
1.看到这里了就点个在看支持下吧,你的在看是我创作的动力。
2.关注公众号,每天为您分享原创或精选文章!
3.特殊阶段,带好口罩,做好个人防护。
